
Patrick Favre-Bulle
Lead Developer
Als Alternative oder auch Ergänzung zu meinem Blogartikel könnt ihr nachfolgend direkt euch meinen dazugehörigen Vortrag im Rahmen der StreamedCon ansehen:
Advanced Encryption Standard
AES, auch bekannt unter seinem ursprünglichen Namen Rijndael, wurde im Jahr 2000 vom National Institute of Standards and Technology (NIST) ausgewählt als ein sichererer Nachfolger für den alten Data Encryption Standard (DES). AES ist ein Blockcipher, d.h. die Verschlüsselung erfolgt auf Bitgruppen fixer-Länge, wobei die Blocklänge auf 128-Bit und die Schlüssellängen auf 128, 192 oder 256 Bit beschränkt wird.
Jeder Block durchläuft viele Runden von Transformationen. Ich werde die Einzelheiten des Algorithmus hier weglassen, aber den interessierten Leser kann ich auf den ausführlichen Wikipedia-Artikel über AES verweisen. Wichtiger Fakt ist, dass die Schlüssellänge keinen Einfluss auf die Blockgröße hat, sondern auf die Anzahl der Wiederholungen der Transformationen (128 Bit Schlüssel haben 10 Zyklen, 256 Bit haben 14).
Until May 2009, the only successful published attacks against the full AES were side-channel attacks on some specific implementations. (Source)
Was ist, wenn wir mehr als einen Block haben?
AES an sich kann nur 128 Bit-Daten verschlüsseln. Wenn wir also ganze Nachrichten verschlüsseln wollen, müssen wir uns sogenannte “Block Mode of Operation” zur Hilfe nehmen. Der einfachste Blockmodus ist das Electronic Codebook oder ECB. Dabei wird für jeden solchen Block derselbe, unveränderte Schlüssel verwendet:
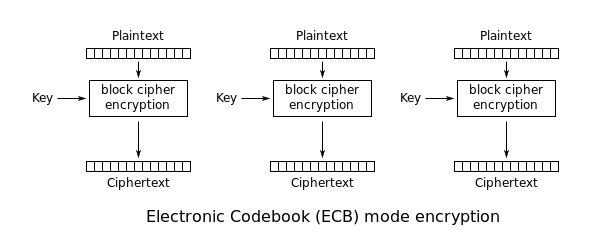
Bild von Wikpedia
Das ist insofern schlecht, da gleiche, unverschlüsselte Blöcke zu gleichen, verschlüsselten werden. Dies führt dazu, dass man gewisse Mustern erkennen kann (das Bild wurde mit ECB verschlüsselt – gern selbst einmal probieren):

Diesen Modus sollte man daher nie wählen, es sei denn, man verschlüsselt nur Daten, die kleiner als 128 Bit sind. Leider wird er trotzdem immer wieder eingesetzt, weil er keinen Initialization Vector erfordert (mehr dazu später) und daher für einen Entwickler einfacher zu handhaben scheint.
Ein Fall muss allerdings mit Blockmodi behandelt werden: Was passiert, wenn der letzte Block nicht genau 128 Bit lang ist? An dieser Stelle kommt Padding ins Spiel, d.h. die fehlenden Bits des Blocks werden nach den Regeln eines Algorithmus aufgefüllt. Im einfachsten Fall werden die fehlenden Bits einfach mit “Zeros” aufgefüllt. Es gibt praktisch keine Sicherheitsauswirkung bei der Wahl der Paddings in AES, deswegen gehe ich hier auch nicht im Detail darauf ein.
Cipher Block Chaining (CBC)
Welche Alternativen zur ECB gibt es also? Zum einen gibt es CBC Modus, der den aktuellen Plaintext Block mit dem vorherigen Ciphertext Block per XOR-verknüpft. Auf diese Weise hängt jeder Plaintext Block von allen bis dahin verarbeiteten Ciphertext-Blöcken ab. Würde man dasselbe Bild wie vorher verwenden, wäre das Ergebnis ein Rauschen, das sich nicht von Zufallsdaten unterscheiden lässt:

Aber was machen wir mit dem ersten Block? Am einfachsten ist es einen Block voller z.B. “Zeros” zu verwenden, aber dann würde jede Verschlüsselung mit dem gleichen Schlüssel und Plaintext den gleichen Ciphertext erzeugen. Ein besserer Weg ist die Verwendung eines zufälligen Initialisierungsvektors (IV). Dies ist nur ein schickes Wort für zufällige Daten, die etwa die Größe eines Blocks (128 Bit) haben. Man kann den IV den “Salt” der Verschlüsselung nennen, d.h. ein IV kann öffentlich sein, sollte zufällig sein und nur einmal verwendet werden. Bei CBC schütz der IV aber nur den ersten Block, da der Ciphertext XORed wird nicht der Plaintext. Wenn man verschlüsselte Daten persistiert oder übermittelt, ist es üblich, den IV an den Ciphertext anzuhängen.
Counter Mode (CTR)
Eine weitere Möglichkeit ist die Verwendung des CTR-Modus. Dieser Blockmodus ist interessant, weil er eine Blockcipher in eine Streamcipher verwandelt. Der Vorteil ist, da man auf beliebige Byte Längen arbeiten kann, dass man kein Padding braucht. In seiner Grundform sind alle Blöcke von 0 bis n durchnummeriert. Jeder Block wird nun mit dem Schlüssel, dem IV (hier auch nonce – “number used once” genannt) und dem Counter verschlüsselt.
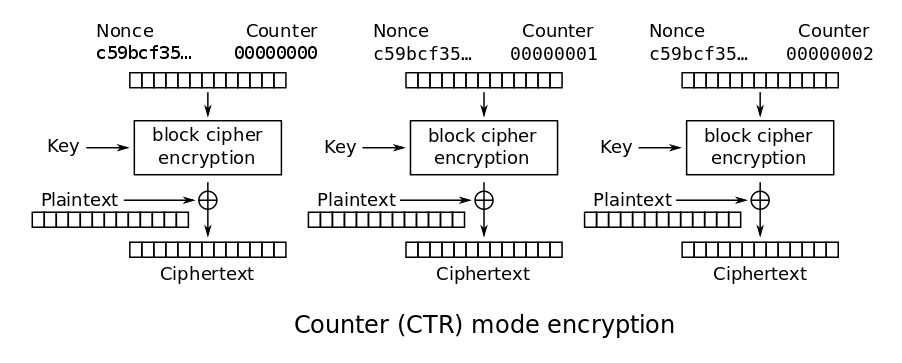
Bild von Wikpedia
Im Gegensatz zu CBC kann die Verschlüsselung parallel erfolgen und alle Blöcke sind vom IV abhängig, nicht nur der erste. Bei der Handhabung ist wichtig, dass man den IV niemals mit dem gleichen Schlüssel wiederverwendet, da ein Angreifer daraus trivial den verwendeten Schlüssel berechnen könnte.
Kann ich mir sicher sein, dass niemand meine Nachricht verändert hat?
Eine Verschlüsselung schützt nicht automatisch vor Datenveränderung von außen, was leider eine sehr übliche Angriffsform ist (siehe ausführlichere Diskussion zu dem Thema).
Was können wir also tun? Wir fügen einfach einen Message Authentication Code (MAC) zur verschlüsselten Nachricht hinzu. Ein MAC ist einer digitalen Signatur ähnlich, mit dem Unterschied, dass der Verifizierungs- und Authentifizierungsschlüssel praktisch derselbe ist. Es gibt verschiedene Varianten dieser Methode, der Modus, der von den meisten Forschern empfohlen wird, heißt Encrypt-then-Mac. Das bedeutet, dass nach der Verschlüsselung ein MAC auf dem Ciphertext berechnet und angehängt wird. Als MAC-Typ wird normalerweise Hash-basierter Nachrichten-Authentifizierungscode (HMAC) verwendet.
Jetzt beginnt es kompliziert zu werden: Für Integrität/Authentizität müssen wir einen MAC-Algorithmus wählen, einen Verschlüsselungs-Tag-Modus wählen, den MAC berechnen und anhängen. Dies ist auch recht langsam, da die gesamte Nachricht zweimal verarbeitet werden muss. Die Gegenseite hat zum Entschlüsseln und Verifizieren natürlich dieselbe Arbeit.
Authenticated Encryption mit GCM
Wäre es nicht toll, wenn es Modi gäbe, die die Komplexität der Authentifizierung für einen erledigen würden? Glücklicherweise gibt es die sogenannte “Authenticated Encryption“, welche gleichzeitig die Vertraulichkeit, Integrität und Authentizität der Daten sicherstellt. Einer der beliebtesten Blockmodi, der dies unterstützt, heißt *Galois/Counter Mode oder kurz GCM* (dieser ist z.B. auch als Cipher Suite in TLS v1.2 verfügbar).
GCM ist im Grunde genommen der CTR-Modus, bei dem während der Verschlüsselung auch ein Authentifizierungs-Tag sequentiell berechnet wird. Dieses Authentifizierungs-Tag wird dann normalerweise an den Ciphertext angehängt. Seine Größe ist eine wichtige Sicherheitseigenschaft, daher sollte er mindestens 128 Bit lang sein.
Es ist auch möglich, zusätzliche Informationen zu authentifizieren, die nicht im Klartext enthalten sind. Diese Daten werden Associated Data genannt. Warum ist dies nützlich? Wenn es Metadaten gibt, z.B. das Erstellungsdatum, kann man leicht überprüfen, ob ein Angreifer diesen Wert verändert hat, ohne dass dieser geheim sein muss.
Eine hitzige Diskussion: 128bit vs. 256bit Schlüssellänge
Intuitiv würde man meinen: Je größer, desto besser – logischerweise ist es schwieriger einen 256-Bit-Zufallswert zu brute forcen als einen 128-Bit-Zufallswert. Nach aktuellem Stand würde es aber astronomisch viel Energie erfordern alle Werte aus einem 128 Bit Wertebereich zu iterieren. Deswegen ist hier der Vergleich eher aus unendlich und unendlich mal 2¹²⁸.
AES actually has three distinct key sizes because it has been chosen as a US Federal Algorithm Apt at being used in various areas under the control of the US federal government [including the military]. (…) So the fine military brains came up with the idea that there should be** three** ”security levels”, so that the most important secrets were encrypted with the heavy methods that they deserved, but the data of lower tactical value could be encrypted with more practical, if weaker, algorithms. (…) So the NIST decided to formally follow the regulations (ask for three key sizes) but to also do the smart thing (the lowest level had to be unbreakable with foreseeable technology). (Source)
Eine AES-verschlüsselte Nachricht wird daher wahrscheinlich nicht durch brute forcen des Schlüssels gebrochen, sondern durch andere, weniger kostspielige Angriffe (welche uns derzeit nicht bekannt sind). Diese Angriffe werden für den 128-Bit-Schlüsselmodus genauso schädlich sein wie für den 256-Bit-Modus, so dass die Wahl einer größeren Schlüsselgröße in diesem Fall nicht viel helfen wird.
Grundsätzlich ist ein 128-Bit-Schlüssel also genug Sicherheit für die meisten Anwendungsfälle mit Ausnahme von Quantencomputerschutz. 128 Bit hat auch Vorteile – es verschlüsselt schneller als mit 256 Bit, und die Key Schedule für 128-Bit-Schlüssel scheint besser geschützt zu sein gegen Related Key Attacks (dies ist jedoch für die meisten Anwendungen in der realen Welt irrelevant).
Zusammenfassung
Es gibt 3 Eigenschaften, die wir uns für die Verschlüsselung unserer Daten wünschen
- Vertraulichkeit: Verhindern, dass Lauschangreifer die Nachricht im Klartext erhalten.
- Integrität: Wenn jemand die Nachricht verändert hat, soll das der Adressat bemerken können.
- Authentizität: Nachweis darüber wer die Nachricht verfasst hat.
AES mit Galois/Counter Mode (GCM)-Blockmodus bietet all diese Eigenschaften, ist relativ einfach zu benutzen und steht in den SDKs der meisten Programmiersprachen zur Verfügung.
